カンガルー法について
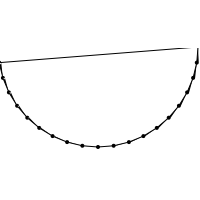
カンガルー法は多角形と様々な図形との交点を高速に求める手法です。具体的には多角形と直線、多角形と円、多角形どうしの交点を求める方法をここでは書きます。それ以外の図形でも線分との距離が求めることのできる図形ならこの手法を応用することができます。カンガルー法のいいところは多角形の辺長の最大置というたった一つのパラメーターを多角形に追加するだけで、いいということです。よって、メモリが節約できますし、コーディングも簡単です。欠点としては多角形の形が"整っていない"場合に適用するとアルゴリズムが非常に非効率的になってしまうことです。具体的には下図のような図形には使いものになりません。
カンガルー法を用いた多角形と直線との交点の高速算出
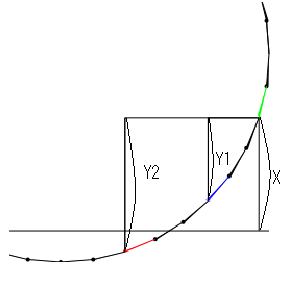
まず、カンガルー法を用いずに素朴に多角形と直線の交点を求める方法を考えてみましょう。多角形の一辺一辺と直線が交わるかを調べれば、答えが出るでしょう。しかし、この方法だと多角形の辺の下図をnとするとO(n)の時間がかかります。一辺一辺を調べずに辺を飛び飛びに調べればより速く交点を求めることができるということは誰でも考えつくことでしょう。それを実現する方法がカンガルー法です。下図をみてください。
図の黄緑色の線が現在直線と交わるか調べている辺とします。この辺と直線との距離がXです。黄緑の線から青の線に進むのは直線を飛び越えないので大丈夫です。しかし、赤の線まで飛び越えてしまうと交点を漏らしてしまいます。ではどのように進めば交点を飛び越えないですむでしょうか。まず、多角形の辺をk個進んだとして、その時に直線の方向にY進んだとします。多角形の辺の最大長をlとしたとき明らかにY<=klが成り立ちます。よって飛び越えないためにはkをX/lを越えない最大の整数にすれば大丈夫に思えます。しかし、一つ飛び越えたということは交わったということなので実際には(X/l+1)を越えない最大の整数にすればいいのです。
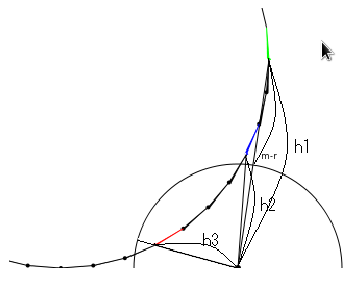
カンガルー法を用いた多角形と円との交点の高速算出
カンガルーメソッドを用いた多角形と円との交点の算出方法は多角形と直線との交点の算出方法と大差ありません。
円と多角形の辺との距離は多角形の辺から円の中心までの距離をmとし、円の半径をrとするとm-rになります。よって飛び越えないためには((m-r)/l+1)をこえない最大の整数だけ多角形の辺を進めればよいです。